leetcode_day64

今日内容：

• Floyd
• A*

Floyd

题目

一个公司在全国有 n 个分部，它们之间有的有道路连接。一开始，所有分部通过这些道路两两之间互相可以到达。

公司意识到在分部之间旅行花费了太多时间，所以它们决定关闭一些分部（也可能不关闭任何分部），同时保证剩下的分部之间两两互相可以到达且最远距离不超过 maxDistance 。

两个分部之间的 距离 是通过道路长度之和的 最小值 。

给你整数 n ，maxDistance 和下标从 0 开始的二维整数数组 roads ，其中 roads[i] = [ui, vi, wi] 表示一条从 ui 到 vi 长度为 wi的 无向 道路。

请你返回关闭分部的可行方案数目，满足每个方案里剩余分部之间的最远距离不超过 maxDistance。

注意，关闭一个分部后，与之相连的所有道路不可通行。

注意，两个分部之间可能会有多条道路。

思路

枚举每种关闭方案，使用Floyd求最短路，然后判断是否合法。

详见代码注释

代码

class Solution {
public:
    //跟敲学习，行行注释
    int numberOfSets(int n, int maxDistance, vector<vector<int>>& roads) {
        vector<vector<int>> matrix(n, vector<int>(n, INT_MAX / 2));//floyd需要的邻接矩阵
        for(auto & road : roads) {//根据roads，初始化邻接矩阵
            int x = road[0], y = road[1], weight = road[2];//路径两端xy，weight为路的权重
            matrix[x][y] = min(matrix[x][y], weight);
            matrix[y][x] = min(matrix[y][x], weight);//无向图，视作两条有向边
        }

        vector<vector<int>> f(n);//去掉一些节点后的邻接矩阵
        auto check = [&](int s) -> bool {//lambda表达式，相当于bool check(int s){}，同时外部变量都可访问
            for(int i = 0;i < n;i++) {//参数s的前n位代表是否取这一个节点
                if((s >> i) & 1) {//若s的i位为1，则取
                    f[i] = matrix[i];//只将保留的节点信息保存，去掉的都变成了无穷
                }
            }

            for(int k = 0;k < n;k++) {//遍历n个节点，进行插值
                if(((s >> k) & 1) == 0) continue;//若s的k位为0，不选
                for(int i = 0;i < n;i++) {//k位为1，选择该节点，下一步遍历整个图，检查最优值是否发生变化
                    if(((s >> i) & 1) == 0) continue;//若s的i位为0，不选
                    for(int j = 0;j < n;j++){//检查从i到其他所有节点的最短路是否变化
                        f[i][j] = min(f[i][j], f[i][k] + f[k][j]);//维护
                    }
                }
            }
            //检查s对应的选择情况，是否满足条件
            for(int i = 0;i < n;i++) {
                if(((s >> i) & 1) == 0) continue;//没选，跳过
                for(int j = 0;j < i;j++) {//无向图，靠后的节点覆盖靠前的节点，邻接矩阵变三角矩阵
                    if((s >> j) & 1 && f[i][j] > maxDistance) {
                        return false;
                    }
                }
            }
            return true;
        };
        int ans = 0;
        for(int s = 0;s < (1 << n);s++) {//枚举子集
            ans += check(s);
        }
        return ans;
    }
};

A-star

题目

在象棋中，马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标，要求根据骑士的移动规则，计算从起点到达目标点所需的最短步数。

棋盘大小 1000 x 1000（棋盘的 x 和 y 坐标均在 [1, 1000] 区间内，包含边界）

输入描述

第一行包含一个整数 n，表示测试用例的数量，1 <= n <= 100。

接下来的 n 行，每行包含四个整数 a1, a2, b1, b2，分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。

输出描述

输出共 n 行，每行输出一个整数，表示骑士从起点到目标点的最短路径长度。

提示信息

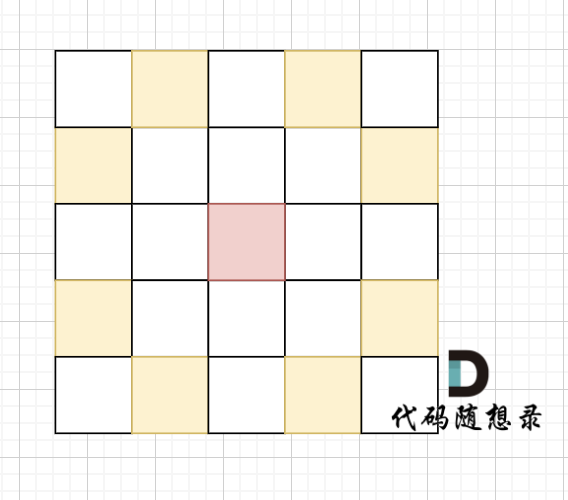
骑士移动规则如图，红色是起始位置，黄色是骑士可以走的地方。

盗链随想录

思路

推荐看随想录的图： 代码随想录 | A-star

A*是启发式搜索，一开始知道要去的地方在哪里，所以根据终点位置，和具体的题目情景，选择合适的距离计算方式(曼哈顿、欧拉、切比雪夫、信息熵……)，根据距离来选择下一步怎么走。

代码

#include<iostream>
#include<queue>
#include<string.h>
using namespace std;
int moves[1001][1001];
int dir[8][2]={-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2,-1,-2};
int b1, b2;
// F = G + H
// G = 从起点到该节点路径消耗
// H = 该节点到终点的预估消耗

struct Knight{
    int x,y;
    int g,h,f;
    bool operator < (const Knight & k) const{  // 重载运算符， 从小到大排序
     return k.f < f;
    }
};

priority_queue<Knight> que;

int Heuristic(const Knight& k) { // 欧拉距离
    return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2); // 统一不开根号，这样可以提高精度
}
void astar(const Knight& k)
{
    Knight cur, next;
	que.push(k);
	while(!que.empty())
	{
		cur=que.top(); que.pop();
		if(cur.x == b1 && cur.y == b2)
		break;
		for(int i = 0; i < 8; i++)
		{
			next.x = cur.x + dir[i][0];
			next.y = cur.y + dir[i][1];
			if(next.x < 1 || next.x > 1000 || next.y < 1 || next.y > 1000)
			continue;
			if(!moves[next.x][next.y])
			{
				moves[next.x][next.y] = moves[cur.x][cur.y] + 1;

                // 开始计算F
				next.g = cur.g + 5; // 统一不开根号，这样可以提高精度，马走日，1 * 1 + 2 * 2 = 5
                next.h = Heuristic(next);
                next.f = next.g + next.h;
                que.push(next);
			}
		}
	}
}

int main()
{
    int n, a1, a2;
    cin >> n;
    while (n--) {
        cin >> a1 >> a2 >> b1 >> b2;
        memset(moves,0,sizeof(moves));
        Knight start;
        start.x = a1;
        start.y = a2;
        start.g = 0;
        start.h = Heuristic(start);
        start.f = start.g + start.h;
		astar(start);
        while(!que.empty()) que.pop(); // 队列清空
		cout << moves[b1][b2] << endl;
	}
	return 0;
}