leetcode_day47

本文最后更新于 2024年7月8日 下午

今日内容：

1143. 最长公共子序列

题目：

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

  • 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

思路：

有两个string，公共子序列出现的地方可能不同，需要i和j两个变量来记录公共子序列在两个string里的范围，以范围逐渐扩张来实现状态的不断推进，二维动态规划。

1. 确定dp数组含义

\(dp[i][j]\)表示字符串\(text_1\)长度为i的前缀，即\(text1[0:i]\)，和\(text_2\)长度为j的前缀的最长公共子序列的长度。

2. 确定状态转移方程

\[ dp[i][j]\ = \begin{cases} dp[i-1][j-1]+1, & \text{$text_1[i-1]=text_2[j-1]$} \\ max(dp[i-1][j],\ dp[i][j-1]), & \text{$text_1[i-1]≠text_2[j-1]$} \end{cases} \]

解释：

  • 当\(text_1[i-1]=text_2[j-1]\)时，\(text_1\)长度为\(i\)的前缀结尾与\(text_2\)长度为\(j\)的前缀结尾相同，在长度为\(i-1\)和\(j-1\)的最长公共子序列基础上再加一，即\(dp[i-1][j-1]+1\)
  • 当\(text_1[i-1]≠text_2[j-1]\)时，相当于末尾没对上，这时不能在之前的基础上加一，需要继承之前的结果，而之前有两个前缀：
    • \(text_1[0:i-1]\)和\(text_2[0:j]\)的最长公共子序列
    • \(text_2[0:j-1]\)和\(text_1[0:i]\)的最长公共子序列
  • 取其中最大值。

3. 初始化

为了方便初始化，dp数组的大小设置成了\((text_1.size()+1)*(text_2.size()+1)\)表示一个左闭右开的区间，同时也以下标表示前缀长度。

此时\(dp[0][0]\)实际无意义，所以初始化\(0\)，遍历都从\(0\)开始。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
        for(int i = 1;i <= text1.size();i++) {
            for(int j = 1;j <= text2.size();j++) {
                if(text1[i - 1] != text2[j - 1]) {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
                else {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
            }
        }
        return dp[text1.size()][text2.size()];
    }
};

1035. 不相交的线

题目：

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足：

  • nums1[i] == nums2[j]
  • 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

盗链lc

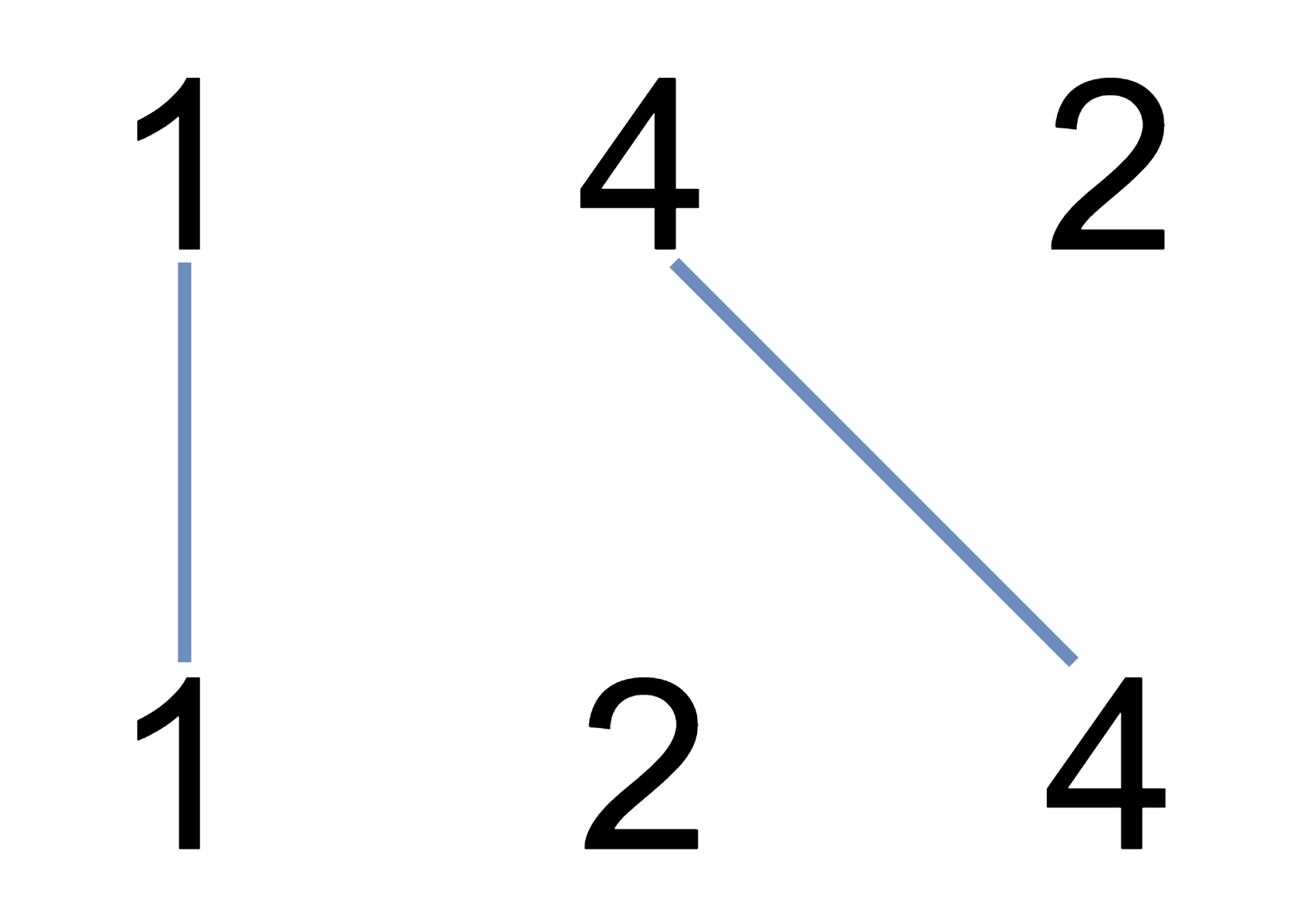
思路：

看图就会发现，这简直就是上一道题换皮，直接套代码就行。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        //换皮最长公共子序列
        vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));

        for(int i = 1;i <= nums1.size();i++) {
            for(int j = 1;j <= nums2.size();j++) {
                if(nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[nums1.size()][nums2.size()];
    }
};

392. 判断子序列

题目：

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：

如果有大量输入的 S，称作 S1, S2, ... , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

思路：

双指针，短的匹配到再走，长的一直走，短的走到头则是子序列。

动态规划：

  • 参考1143题的初始化方法，dp数组初始化为\((s.size()+1)*(t.size()+1)\)，使\(dp[0][0]\)无意义。遍历都从1开始。
  • \(dp[i][j]\)代表\(s[0:i-1]\)和\(t[0:j-1]\)公共子序列长度
  • 状态转移方程为：

\[ dp[i][j]\ = \begin{cases} dp[i-1][j-1]+1, & \text{$s[i-1]=t[j-1], i,j>0$} \\ dp[i][j-1], & \text{$else$} \end{cases} \]

  • 匹配到则推进状态，公共子序列长度加一
  • 未匹配则继承状态，注意\(s\)不前进而\(t\)前进，代表继续在\(t\)中寻找\(s[i]\)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool isSubsequence(string s, string t) {
        if(s.size() > t.size()) return false;
        vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));//开大一个，方便处理0情况
        for(int i = 1;i <= s.size();i++) {
            for(int j = 1;j <= t.size();j++) {
                if(s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;//匹配，i和j都往前走
                else dp[i][j] = dp[i][j - 1];//未匹配，s不能动，t往前走
            }
        }
        return dp[s.size()][t.size()] == s.size();//如果s走到最后，则是
    }
};

53. 最大子数组和

题目：

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

思路：

依据贪心的思路，可以迁移到动态规划来，贪心就是和为负之后，就对之后没有贡献了，直接抛弃，将下一个作为新起点重新计算子数组和，动态规划也可以这样：

  • \(dp[i]\)代表以\(nums[i]\)结尾的最大子数组和
  • 若\(dp[i-1]<0\)，则抛弃，以当前\(nums[i]\)作为新起点：\(dp[i] = nums[i]\)
  • 若\(dp[i-1]>=0\)，则继承结果：\(dp[i] = dp[i-1]+nums[i]\)
  • \(dp[0]\)按意义该初始化为\(nums[0]\)
  • 用一个变量记录其中最大的子数组和

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        vector<int> dp(nums.size(), 0);
        dp[0] = nums[0];
        int ans = dp[0];
        for(int i = 1;i < nums.size();i++) {
            if(dp[i - 1] <= 0) dp[i] = nums[i];
            else dp[i] = dp[i - 1] + nums[i];
            ans = max(dp[i], ans);
        }
        return ans;
    }
};
#leetcode
leetcode_day47
https://novelyear.github.io/2024/07/08/leetcode-day47/
作者
Leoo Yann
更新于
2024年7月8日
许可协议