leetcode_day33

本文最后更新于 2024年8月18日 下午

今日内容：

452. 用最少数量的箭引爆气球

题目：

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中 $points[i] = [x_{start}, x_{end}] $ 表示水平直径在 \(x_{start}\) 和\(x_{end}\)之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为\(x_{start}\)，\(x_{end}\)， 且满足 \(x_{start} ≤ x ≤ x_{end}\)，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

思路：

按照直观思维，肯定要找重叠部分，再按贪心分析，局部最优是射重叠部分，全局最优是尽可能多射重叠部分来减少箭数

此时不妨画个图来分析，脑子好也可以直接想象，用线段表示气球直径范围，以下图为例，很容易看出答案是两根箭，但是我们是如何得出答案的呢，背后的依赖逻辑是什么

帮助分析线段图

此时发散思维，不难想到跟开始和结束点有关，此前做过类似题则更容易想到，以结束点为标准，从左往右开始射，必须照顾到最早结束的气球，否则就会漏掉，那么我们就能得到如下贪心策略：（大白话版）

按起点排序，记录气球结束点按最近的来，若结束点超过了这个最近结束点，则一支箭就不够了。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    static bool cmp(const vector<int> & a, const vector<int> & b) {
        return a[0] < b[0];
    }
    //按起点排序，记录气球结束点按最近的来，若结束点超过了这个最近结束点，则一支箭就不够了
    int findMinArrowShots(vector<vector<int>>& points) {
        sort(points.begin(), points.end(), cmp);
        int end = points[0][1];
        int nextBallon = 0;//新的起点
        int arrow = 1;//箭数
        for(int i = 0;i < points.size();i++) {
            if(end < points[i][0]) {
                nextBallon = i;
                arrow++;
                end = points[i][1];
            }
            end = min(end, points[i][1]);
        }
        return arrow;
    }
};

435. 无重叠区间

题目：

给定一个区间的集合 intervals ，其中 intervals[i] = [start_i, end_i] 。返回需要移除区间的最小数量，使剩余区间互不重叠 。

思路：

由于之前做过一道安排活动的题目，大概意思就是有很多活动(区间)，请在不重叠的前提下安排尽可能多的活动。与此题很像

安排活动题就是按结束时间从早到晚排序，先安排早的，这样就有局部最优：留出更多的时间给之后的活动，如果结束时间相同，则为了多，选择更短的活动，以留出更多时间给更早的活动

那么这道题也可以迁移这个策略，移除最少就是保留最多嘛。

这道题比较经典，carl给了很多思路，建议阅读：代码随想录 | 无重叠区间

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    static bool cmp(const vector<int> & a, const vector<int> & b) {
        return a[1] == b[1] ? a[0] > b[0] : a[1] < b[1];
    }
    //移除最少那就保留最多，移除长的，保留短的
    //保留最多就要流出足够多的时间给后面的区间，所以结束时间要早
    //那么应该按结束时间排序，如果结束相同，那么选择开始时间最晚的
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), cmp);
        int end = intervals[0][1];
        int save = 1;//保留的活动数
        for(int i = 1;i < intervals.size();i++) {
            if(intervals[i][0] < end) continue;
            else {
                save++;
                end = intervals[i][1];
            }
        }
        return intervals.size() - save;
    }
};

763. 划分字母区间

题目：

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

思路：

一开始有点懵，然后迁移之前的思路想到可以将字母出现的范围视作区间，那就又成了区间不重叠问题。

但这个思路编码有点复杂，速度也不快

carl的直截了当思路简直优雅👍:

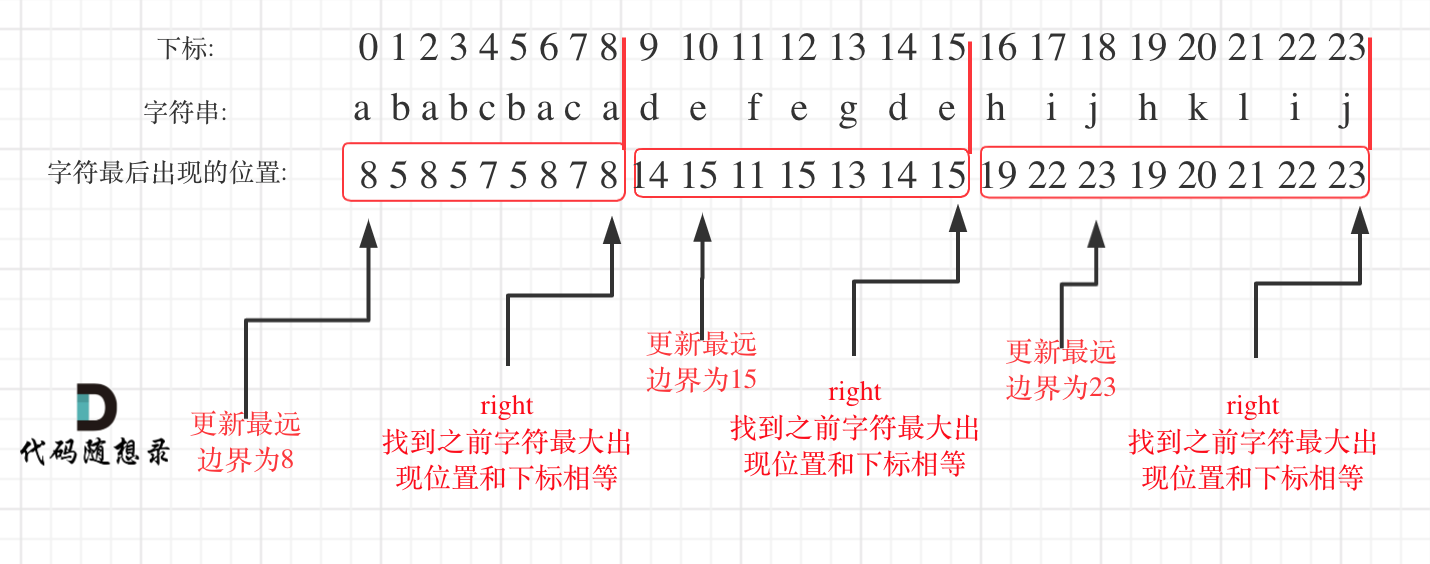
  • 统计每一个字符最后出现的位置
  • 从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点
太巧妙辣！

代码

个人14%代码😭

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    static bool cmp(const vector<int> & a, const vector<int> b) {
        return a[0] < b[0];
    }
    //尽可能多的片段，且是分割，是连续的，只在前面出现的字母，统计各字母首次和默次出现构成区间
    //按区间开始排序，目的是分出尽可能多的组，原理相同
    vector<int> partitionLabels(string s) {
        vector<vector<int>> points;//存各字母的区间
        vector<int> ans;
        //获取s中各字母的区间
        points = getSection(s);
        //写代码能力太弱，有点费时间啊……
        sort(points.begin(), points.end(), cmp);
        int right = points[0][1], left = 0;
        for(int i = 1;i < points.size();i++) {
            if(points[i][0] > right) {
                ans.push_back(right - left + 1);
                left = points[i][0];
            }
            right = max(right, points[i][1]);
        }
        ans.push_back(right - left + 1);
        return ans;
    }
    vector<vector<int>> getSection(string s) {
        vector<vector<int>> alpha(26, vector<int>(2, -1));//全部字母都留出空
        vector<vector<int>> res;
        for(int i = 0;i < s.size();i++) {
            if(alpha[s[i] - 'a'][0] == -1) alpha[s[i] - 'a'][0] = i;//起点只记一次
            alpha[s[i] - 'a'][1] = i;//终点不断更新
        }
        for(int i = 0;i < alpha.size();i++) {
            if(alpha[i][0] != -1) res.push_back(alpha[i]);//结果只记录出现过的
        }
        return res;
    }
};

carl优雅代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int> partitionLabels(string S) {
        int hash[27] = {0}; // i为字符，hash[i]为字符出现的最后位置
        for (int i = 0; i < S.size(); i++) { // 统计每一个字符最后出现的位置
            hash[S[i] - 'a'] = i;
        }
        vector<int> result;
        int left = 0;
        int right = 0;
        for (int i = 0; i < S.size(); i++) {
            right = max(right, hash[S[i] - 'a']); // 找到字符出现的最远边界
            if (i == right) {
                result.push_back(right - left + 1);
                left = i + 1;
            }
        }
        return result;
    }
};
#leetcode
leetcode_day33
https://novelyear.github.io/2024/07/01/leetcode-day33/
作者
Leoo Yann
更新于
2024年8月18日
许可协议