leetcode_day28

本文最后更新于 2024年8月18日 下午

期末复习压力大，简单写写，暑假再补

(已补)

今日内容：

491. 非递减子序列

题目：

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

思路：

难点在于去重，例如[1,2,3,1,1]这样的用例，就要注意不要在解空间树第一层重复取1，最后得到重复的[1,1]和[1,1,1]，解空间树单层去重方法为在单层递归中创建一个作用域仅限于单层递归函数内的记录变量数组，用过就记录，之后再用就跳过，具体代码实现方法见下

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<vector<int>> ans;
    vector<int> temp;
    int pre = -101;
    void backtrack(vector<int> & nums, int begin) {
        if(temp.size() >= 2) {
            ans.push_back(temp);
        }
        vector<bool> used(210, false);//这就是作用域仅在单层的记录变量
        for(int i = begin;i < nums.size();i++) {
            if(nums[i] < pre) continue;
            if(used[nums[i] + 100]) continue;
            used[nums[i] + 100] = true;
            temp.push_back(nums[i]);
            pre = nums[i];
            backtrack(nums, i + 1);
            temp.pop_back();
            pre = !temp.empty() ? temp.back() : -101;
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtrack(nums, 0);
        return ans;
    }
};

46. 全排列

题目：

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

思路：

在程序设计课上写那么久，之前一直踩坑全局used，这下终于能尽情全局used了，手速题，10min秒了

carl哥的方法明明和我一样，只是把used下传了，但就是快，也许是语法因素？

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<bool> used;
    vector<vector<int>> ans;
    vector<int> temp;
    void backtrack(vector<int> &nums){
        if(temp.size() == nums.size()) {
            ans.push_back(temp);
            return;
        }
        for(int i = 0;i < nums.size();i++) {
            if(used[i]) continue;
            used[i] = true;
            temp.push_back(nums[i]);
            backtrack(nums);
            temp.pop_back();
            used[i] = false;
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        used.resize(nums.size(), false);
        backtrack(nums);
        return ans;
    }
};

47. 全排列Ⅱ

题目：

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

思路：

又是去重，由于任意顺序，所以可以排序，对于[1,1,2]这样的用例，需要注意的就是不要来两个[1,1,2]，光把前两个1交换了。

去重标准可设为：相同元素仅允许最先一个作为开头，之后的相同元素不可做开头，但可做后缀。

翻译成代码就是if(i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<vector<int>> ans;
    vector<int> temp;
    vector<bool> used;
    void backtrack(vector<int> &nums) {
        if(temp.size() == nums.size()) {
            ans.push_back(temp);
        }
        for(int i = 0;i < nums.size();i++) {
            if(i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;
            if(used[i]) continue;
            used[i] = true;
            temp.push_back(nums[i]);
            backtrack(nums);
            temp.pop_back();
            used[i] = false;
        }
    }
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        used.resize(nums.size(), false);
        backtrack(nums);
        return ans;
    }
};

332. 重新安排行程

题目：

给你一份航线列表 tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。

所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

例如，行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前。 假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。

思路：

首先看懂题目，类似哥尼斯堡七桥问题，也就是欧拉回路，就是要找到一条路，能把所有路走一遍且不重复，而此题还额外要求字典序最小。

那么可以直观得到如下思路：

  1. 找到当前节点能够去到的 所有 下一个节点，按字典序由小到大排好序
  2. 从最小字典序节点开始dfs，如果最后没能用光机票而走入死路，则换次小字典序节点继续寻找，直到找到。

思路其实不难，主要在于代码实现，carl合理选择了适当的容器来做，代码时间打败98%，但我这次独立完成，主要记录个人解题思路，目前最优解仍为carl的题解，详见：代码随想录 | 重新安排行程。

对于我的思路，具体代码实现遇到的问题见代码注释，直接叙述效果不佳

代码

个人代码（可怜的5%😭）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    vector<string> path;//存欧拉道路
    vector<bool> used;//记录哪些tickets的下标已经被用过，即用过的机票
    bool backtrack(vector<vector<string>> &tickets, string start) {
        if(path.size() == tickets.size() + 1) return true;
        //根据start得到接下来的目标，选取可用的机票，按字典序从小到大排列
        //按下标存方便used记录，按名称存不好记录哪些机票用过了，后续会出问题，于是两个合在一起存，排序自定义
        vector<pair<int, string>> nextPort;
        for(int i = 0;i < tickets.size();i++) {
            if(!used[i] && tickets[i][0] == start) {
                nextPort.push_back(pair<int, string>(i, tickets[i][1]));
            }
        }
        sort(nextPort.begin(), nextPort.end(), cmp);
        //遍历接下来的机场，如果找到答案，则直接返回，如果没有，则换次小字典序机场再找
        for(int i = 0;i < nextPort.size();i++) {
            if(used[nextPort[i].first]) continue;
            //超时尝试剪枝，对于相同机票，可失败后跳过后续所有相同机票
            //剪枝后成功AC，但用时仅超过5%，丢人
            if(i > 0 && nextPort[i].second == nextPort[i - 1].second) continue;
            used[nextPort[i].first] = true;
            path.push_back(nextPort[i].second);
            if(backtrack(tickets, nextPort[i].second)) return true;
            path.pop_back();
            used[nextPort[i].first] = false;
        }
        //如果走到这一步，证明走错，返回false
        return false;
    }
    static bool cmp(const pair<int, string> a, const pair<int, string> b) {
        return a.second.compare(b.second) < 0;//按照字典序排序
    }
    vector<string> findItinerary(vector<vector<string>>& tickets) {
        used.resize(tickets.size(), false);//记录哪些机票已经被用过
        path.push_back("JFK");//起点不会被加入，所以提前加入
        backtrack(tickets, "JFK");
        return path;
    }
};

carl的优质代码个人注释版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
private://才注意到carl哥把自己实现的方法都private了，细节！
// unordered_map<出发机场, map<到达机场, 航班次数>> targets
unordered_map<string, map<string, int>> targets;// 起点 -> (目的地，剩余可飞次数)
bool backtracking(int ticketNum, vector<string>& result) {
    if (result.size() == ticketNum + 1) {//找齐了
        return true;//回传成功信号，也算剪枝了吧，不用再遍历后续的target了
    }
    for (pair<const string, int>& target : targets[result[result.size() - 1]]) {//细节引用，result[result.size() - 1]就是前一个机场，targets[result[result.size() - 1]]就是要遍历的目的地集合
        if (target.second > 0 ) { // 该路线还有余票
            result.push_back(target.first);//回溯模板，看不懂只能去复习了
            target.second--;
            if (backtracking(ticketNum, result)) return true;
            result.pop_back();
            target.second++;
        }
    }
    return false;
}
public:
    vector<string> findItinerary(vector<vector<string>>& tickets) {
        targets.clear();//细节clear，防止内存里有脏东西
        vector<string> result;//没开成员变量，提高速度，见 全排列的疑惑
        for (const vector<string>& vec : tickets) {//vec就是每张票了，俩元素，起点[0]跟终点[1]
            targets[vec[0]][vec[1]]++; // 这里就提前给每个目的地集合按字典序排好序了，之后从头遍历就行
        }
        result.push_back("JFK"); // 手动加入起始机场
        backtracking(tickets.size(), result);
        return result;
    }
};

51. N皇后

题目：

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

提示：

1 <= n <= 9

思路：

按图的深度优先搜索回溯查找所有放置可能，结束条件就是放到了最后一行仍然合法，放一个就在当前基础上往下搜索，写好判断合法函数，注意有两条斜线，经典问题所以不太难，披着hard的中等题吧。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    vector<vector<string>> ans;//存放所有解
    void backtrack(int n, int row, vector<string> &board) {
        if(row == n) {//最后一行放下去了，来到了界外
            ans.push_back(board);
            return;
        }

        for(int i = 0;i < n;i++) {
            if(!isVaild(n, row, i, board)) continue;
            board[row][i] = 'Q';
            backtrack(n, row + 1, board);
            board[row][i] = '.';//尝试下一个放置位
        }
    }
    bool isVaild(int n, int row, int col, vector<string> &board) {
        for(int r = 0;r < n;r++) {//检测[row, col]有无同列Queen
            if(board[r][col] == 'Q') return false;
        }
        int r = row, c = col;
        while(r >= 0 && c >= 0) {//检测左上斜线有无Queen
            if(board[r--][c--] == 'Q') return false;
        }
        r = row, c = col;
        while(r >= 0 && c < n) {//检测右上斜线有无Queen
            if(board[r--][c++] == 'Q') return false;
        }

        return true;
    }
    vector<vector<string>> solveNQueens(int n) {
        vector<string> board(n, string(n, '.'));
        backtrack(n, 0, board);
        return ans;
    }
};

37. 解数独

题目：

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

  • 数字 1-9 在每一行只能出现一次。
  • 数字 1-9 在每一列只能出现一次。
  • 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

数独部分空格内已填入了数字，空白格用 '.' 表示。

示例一：

示例一 
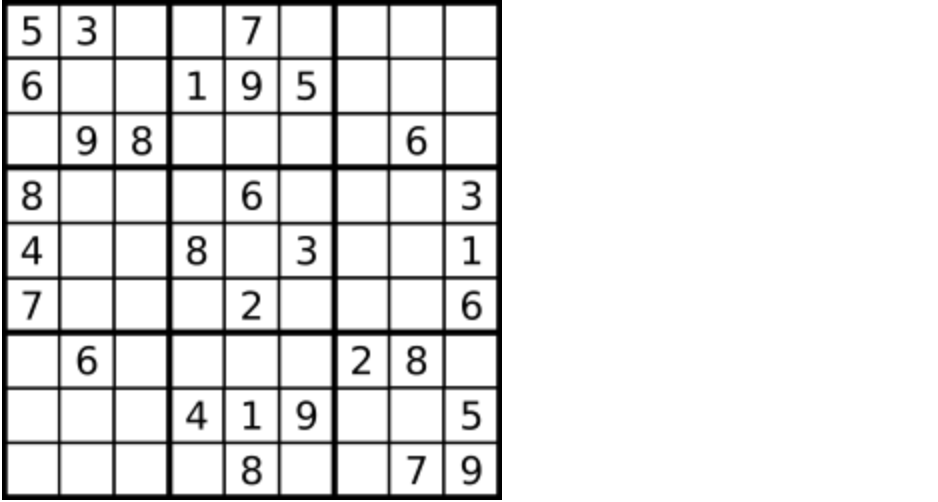
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
输入：board = [["5","3",".",".","7",".",".",".","."],

["6",".",".","1","9","5",".",".","."],

[".","9","8",".",".",".",".","6","."],

["8",".",".",".","6",".",".",".","3"],

["4",".",".","8",".","3",".",".","1"],

["7",".",".",".","2",".",".",".","6"],

[".","6",".",".",".",".","2","8","."],

[".",".",".","4","1","9",".",".","5"],

[".",".",".",".","8",".",".","7","9"]]

输出：[["5","3","4","6","7","8","9","1","2"],

["6","7","2","1","9","5","3","4","8"],

["1","9","8","3","4","2","5","6","7"],

["8","5","9","7","6","1","4","2","3"],

["4","2","6","8","5","3","7","9","1"],

["7","1","3","9","2","4","8","5","6"],

["9","6","1","5","3","7","2","8","4"],

["2","8","7","4","1","9","6","3","5"],

["3","4","5","2","8","6","1","7","9"]]

解释：输入的数独如上图所示，唯一有效的解决方案如下所示：
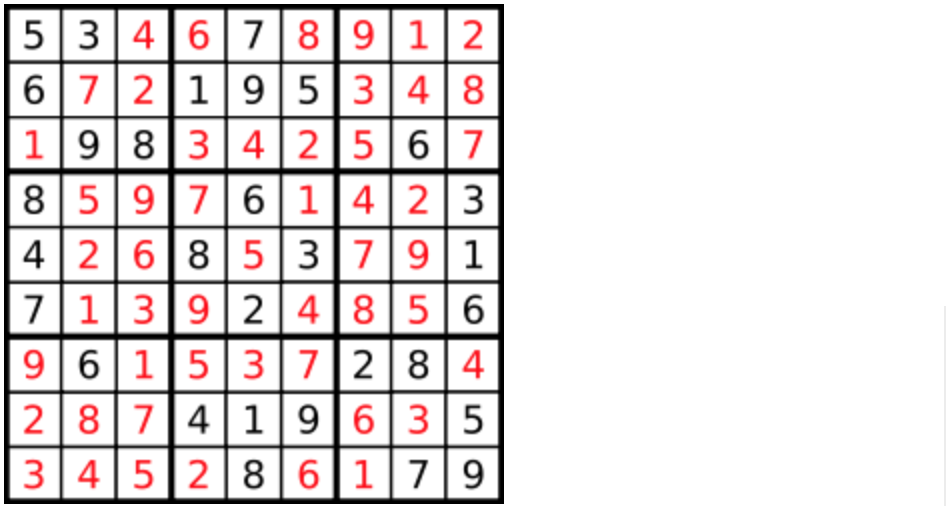
answer

图源：代码随想录

思路：

没写出来，想着用n皇后的思路一个一个回溯暴力填的，结果一堆bug😭

记录一下错误思路：在回溯函数里我传入了上一个被填位置的row和col，想着每次向下递归就能知道上次在哪里，结果会出现：一行填到最后一个没法填了，退回去清空倒数第二格后再跳过把最后一格填了，留着空格子不管直接下一行……

问题出在返回false的时机上，其实到没法填的时候就已经可以返回false了，然后会到上一格接着试下一个数字。

这道题回溯没有单独设置终止条件，如果有传参的话也许可以加一条到了8行9列就返回，不过也可以不加，循环跑完自然就会结束。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    //先行再列，逐个试错
    bool backtrack(vector<vector<char>>& board) {
        for(int r = 0;r < 9;r++) {
            for(int i = 0;i < 9;i++) {//先填满row行
                if(board[r][i] != '.') continue;
                for(int j = 1;j <= 9;j++) {//为(r, i)尝试所有可能数字
                    if(!isValid(board, r, i, j)) continue;
                    board[r][i] = '0' + j;
                    if(backtrack(board)) return true;
                    board[r][i] = '.';
                }
                return false;//没得填了，返回false
            }
        }
        return true;
    }
    bool isValid(vector<vector<char>> & board, int row, int col, int num) {
        for(int c = 0;c < 9;c++) if(board[row][c] == '0' + num) return false;
        for(int r = 0;r < 9;r++) if(board[r][col] == '0' + num) return false;
        for(int r = row / 3 * 3;r < (row / 3 + 1)*3;r++) {//宫格
            for(int c = col / 3 * 3;c < (col / 3 + 1)*3;c++) {
                if(board[r][c] == '0' + num) return false;
            }
        }
        return true;
    }
    void solveSudoku(vector<vector<char>>& board) {
        backtrack(board);
    }
};
#leetcode
leetcode_day28
https://novelyear.github.io/2024/06/19/leetcode-day28/
作者
Leoo Yann
更新于
2024年8月18日
许可协议