leetcode_day27

今日内容：

• 93. 复原IP地址 medium
• 78. 子集 medium
• 90. 子集Ⅱ medium

93. 复原IP地址

题目：

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。 给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

思路：

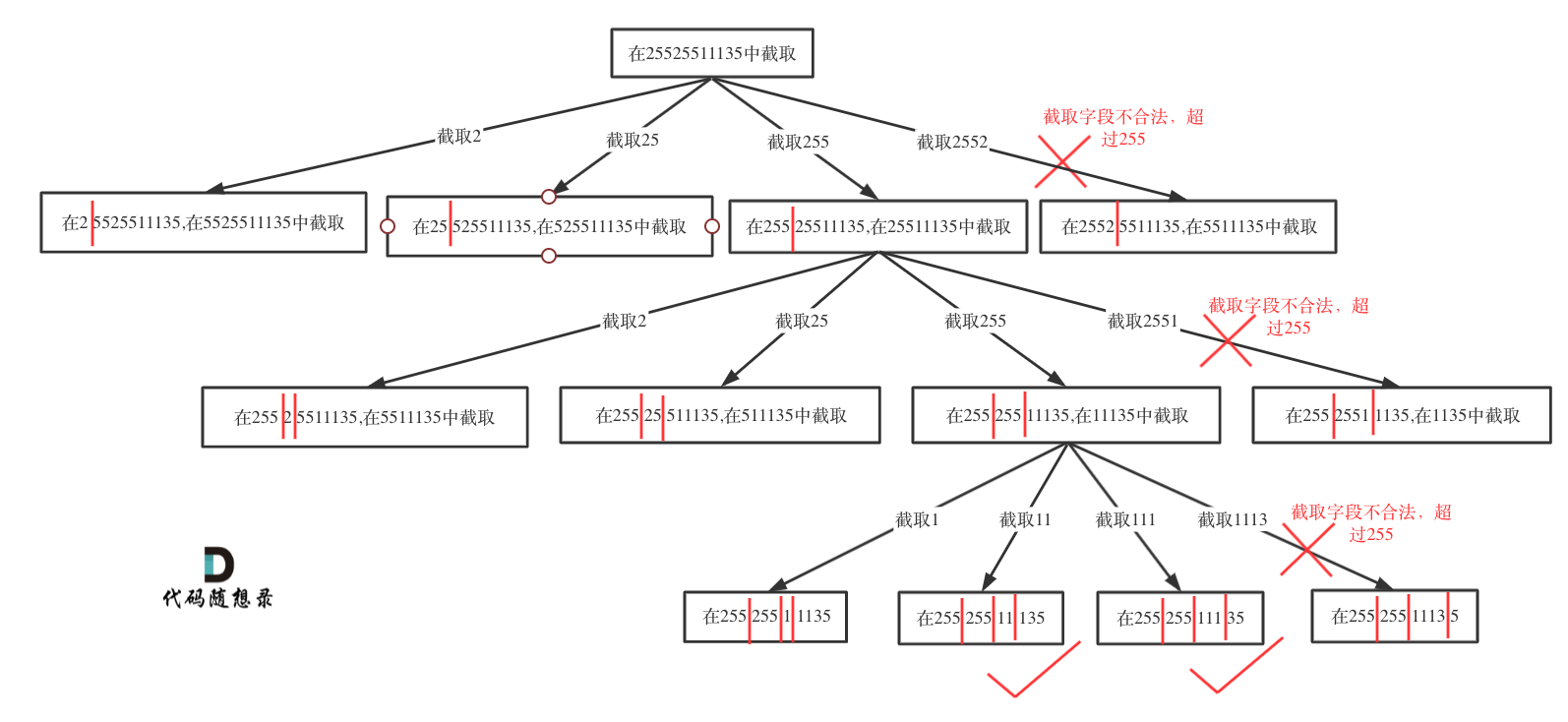
回溯做了几天，对于简单的解空间树怎么分支比较熟悉了，这题就先按长度从1到3分割，然后下传起点，如果第四段仍然合法，则找到一个答案，不断递归回溯寻找所有答案即可。

解空间树.图源：代码随想录

代码

class Solution {
public:
    vector<string> ans;
    string temp;
    int seg = 4;//剩余段数
    void backtrack(string &s, int begin) {
        if(seg < 0) return;
        if(seg == 0 && begin >= s.size()) {
            ans.push_back(temp);
            return;
        }
        for(int i = begin;i < s.size();i++) {
            if(s.size() - i > seg * 3 && i - begin >= 3) break;//后续太多，直接剪枝\提前判断位数剪枝
            if(isValid(s, begin, i)) {
                if(begin > 0) temp.push_back('.');
                temp += string(s.begin() + begin, s.begin() + i + 1);
                seg--;
            }
            else continue;
            backtrack(s, i + 1);
            while(!temp.empty() && temp.back() != '.') temp.pop_back();
            if(!temp.empty()) temp.pop_back();
            seg++;
        }
    }
    bool isValid(string s, int begin, int end) {
        if(begin < end && s[begin] == '0') return false;
        long long num = 0;
        while(begin <= end) {
            num *= 10;
            num += s[begin++] - '0';
        }
        return 0 <= num && num <= 255;
    }
    vector<string> restoreIpAddresses(string s) {
        backtrack(s, 0);
        return ans;
    }
};

78. 子集

题目：

给你一个整数数组 nums ，数组中的元素 互不相同。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

思路：

也是很容易套上模板的回溯，不过不能不求甚解依赖模板，还是要想清楚代码逻辑。这题是求子集，高中就学过n个元素的集合有2^n个子集，虽然跟这没啥关系，不过可以认识到求子集就是求元素个数从0~n的关于全集nums的组合，所以可以分别求长度为i，i从0到n，的组合，那就是从nums里抓i个的组合，就变成了该题的上一题：77. 组合了。

对于错误思路的反思：

注意到该题的tag里有位运算字样，昨天做错的题目里我也尝试使用位运算模拟bool used[]来记录哪些数字已经被使用过，但实际上是多余的。今天又看见位运算，由于其出现在tag里，所以深信不疑，再次尝试，WA，去掉后，AC。下面逐条分析错误核心，搞清楚什么时候用used记录用过，什么时候不用。

for(int i = begin;i < nums.size();i++) {//此处i从begin开始，已经与之前的结果隔开
    if(used >> nums[i] % 2 == 1) continue;//这句等同于：如果nums[i]在之前用过就跳过，但此题nums中无重复元素，所以之前出现的元素之后肯定没出现过，多余
    used |= 1 << nums[i];//在used的第nums[i]位置一
    temp.push_back(nums[i]);
    backtrack(nums, i + 1, len);
    temp.pop_back();
    used &= ~(1 << nums[i]);//第nums[i]位复位
}

看完发现，used的确多余，但好像没有影响啊，其实WA原因在于used >> nums[i] % 2，%运算符优先级高于>>，所以错了。

当然，改了还是会错，nums里有负数，这样就越来越复杂了。

代码

第一版

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> temp;
    void backtrack(vector<int> &nums, int begin, int len) {
        if(temp.size() == len) {
            ans.push_back(temp);
            return;
        }
        for(int i = begin;i < nums.size();i++) {
            temp.push_back(nums[i]);
            backtrack(nums, i + 1, len);
            temp.pop_back();
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        for(int i = 0;i <= nums.size();i++) {

            backtrack(nums, 0, i);
        }
        return ans;
    }
};

carl的解

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> temp;
    void backtrack(vector<int> &nums, int begin) {
        ans.push_back(temp);//提前
        if(begin >= nums.size()) {
            return;
        }
        for(int i = begin;i < nums.size();i++) {
            temp.push_back(nums[i]);
            backtrack(nums, i + 1);
            temp.pop_back();
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        backtrack(nums, 0);
        return ans;
    }
};

90. 子集Ⅱ

题目：

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的 子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

思路：

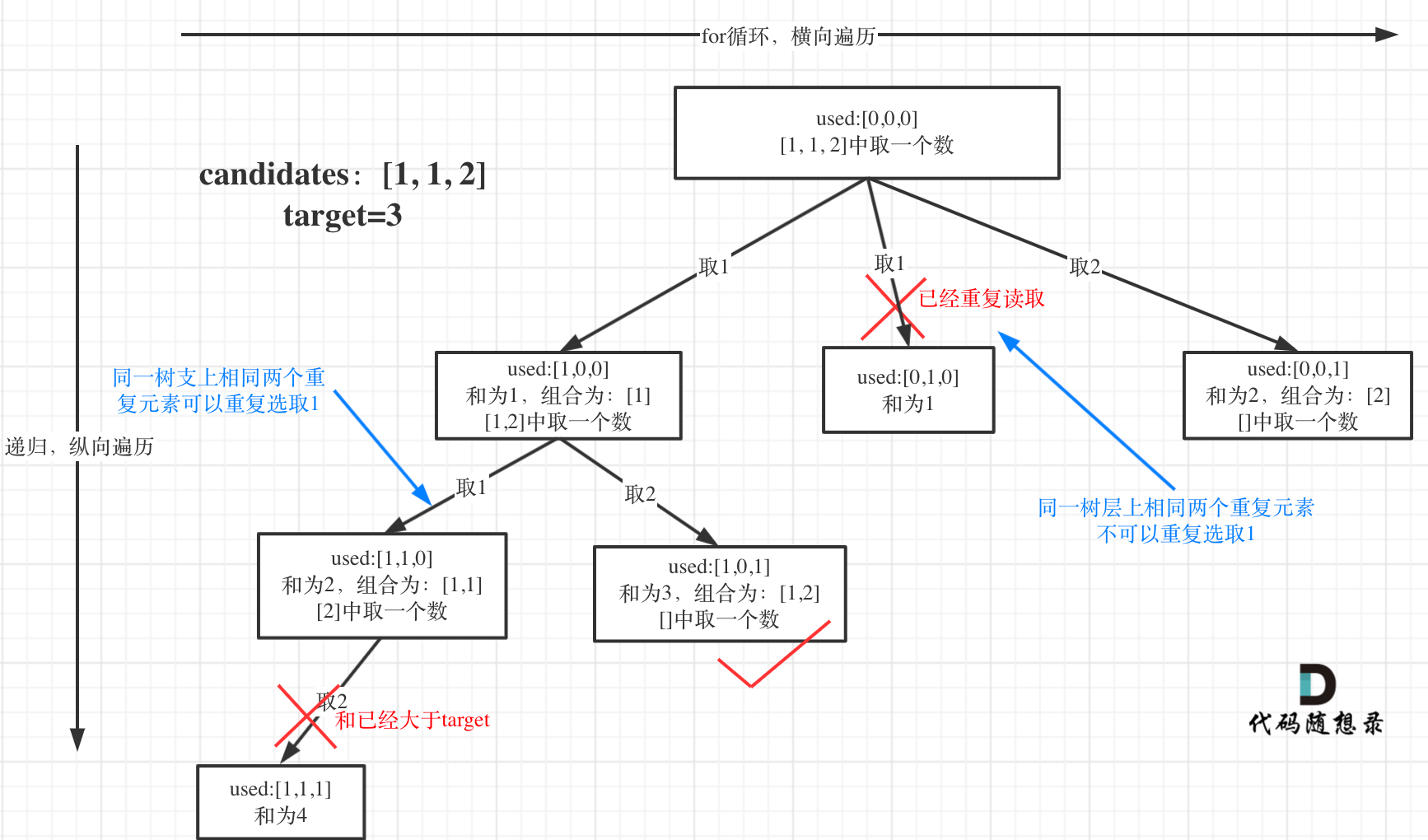
与上一题相比多了重复元素，相当于[1,2,2]的子集注意别回溯出两个[1,2]，可以采用昨天40. 组合总和的相同去重思路。在昨天的blog中已经提到不能简单用used来尝试去重。所以还是乖乖用carl的写法，附图carl的解空间树：

子集Ⅱ解空间树,图源：代码随想录 | 子集Ⅱ

代码

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> temp;
    void backtrack(vector<int> &nums, int begin) {
        ans.push_back(temp);
        if(begin >= nums.size()) {
            return;
        }
        for(int i = begin;i < nums.size();i++) {
            //使用这条的前提是要排序哦，不然相同的不挨在一起就麻烦了
            if(i > begin && nums[i] == nums[i - 1]) continue;
            temp.push_back(nums[i]);
            backtrack(nums, i + 1);
            temp.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        backtrack(nums, 0);
        return ans;
    }
};